Have you ever wondered why we talk about our boat speed and wind speed in knots and not kilometers or miles per hour as we do on land?

It all has to do with the number sixty. 60 is a very important number for navigators. In one degree of latitude, for example, we have 60 minutes. In 60 minutes we have sixty seconds.

If a boat is moving over the ground at one knot, and does so for the next sixty hours, it will have traveled sixty nautical miles.

Positions are expressed in degrees, minutes and seconds, each component having sixty units (sixty degree, sixty minutes and sixty seconds.) When working with paper charts this relationship is more tangible because there are scales and instruments specific to the task of navigating, but when we use computerised chart plotting and GPS all of this is dealt with by the machine and not our heads.

So let me introduce you to the 1 in 60 rule. The 1 in 60 rule adheres to the fact that with a right-angle triangle, and for argument's sake lets say the longest side measures 60 'units,' then the length of the shortest side will be the same in units as the degrees of the angle opposite. Yeah right. I learn by doing, so here's how to apply the rule in your navigation.

Example 1:

When sailing a boat, the wind sometimes (OK, most times) hampers you from being able to set a direct course for your waypoint. Say you are 5 degrees low of your intended mark and that your intended mark is 30 miles off in the distance. If I keep going for 30 miles 5 degrees low of the mark, the question is "how far will I be from the intended mark once I've run 30 miles?"

Use this two step simple formula to find the answer.

So let's use our formulas above to solve a real world problem. You have 30 miles to run to the waypoint and you are pointing 5 degrees low of that mark. How far will I be from the waypoint holding this course?

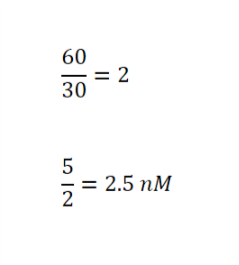
Example 2:

Let's use another example. You have 45 miles to run and are 15 degrees off your intended track.

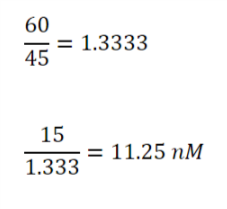
Get it? Nifty eh!

---

Experience Counts!

---